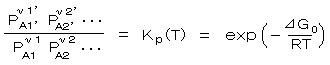丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂揹婥壔妛偺幚尡
丂丂侾丏丂僱儖儞僗僩偺幃
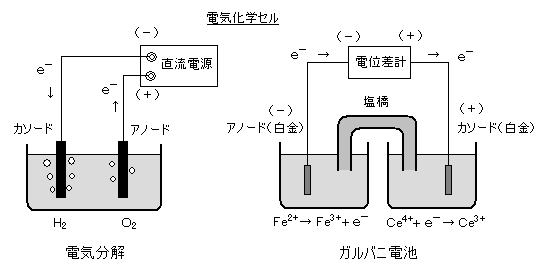
丂丂揹婥壔妛僙儖偼丄侾乯丂揹夝憛丄 俀乯丂僈儖僶僯揹抮 偺俀偮偵戝暿偝傟傞丅丂揹夝憛偱偼丄旕帺敪揑側斀墳偑 奜晹偐傜偺揹婥僄僱儖僊乕偵傛偭偰恑峴偝偣傜傟傞丅乮悈偺揹婥暘夝丄傔偭偒丄揹夝惛楤側偳乯丂堦曽丄僈儖僶僯揹抮乮揹抮偺憤徧乯偼丄壔妛斀墳偑帺敪揑偵恑峴偟丄奜晹偵揹婥僄僱儖僊乕傪嫙媼偡傞丅
丂丂乮仏丂揹嬌偺柤徧偼丄 傾僲乕僪丗 巁壔斀墳偑婲偙傞嬌丄揹夝憛偱偼惓嬌丒僈儖僶僯揹抮偱偼晧嬌丄丂僇僜乕僪丗
娨尦斀墳偑婲偙傞嬌丄揹夝憛偱晧嬌丒僈儖僶僯揹抮偱惓嬌乯
丂丂巁壔懱乮俷倶乯偲 娨尦懱乮俼倕倓乯偲偺娫偺 揹巕庼庴偺暯峵乮亖敿揹抮斀墳偺暯峵乯
丂丂丂丂丂丂丂丂丂丂丂倎 俷倶 亄 値 倕亅 亖 倐 俼倕倓丂丂
偵偮偄偰丄
揹棳偑棳傟偰偄側偄偲偒偺 敿揹抮偺揹嬌揹埵偼丄壔妛億僥儞僔儍儖偺峫偊曽偵婎偯偄偰丄師偺 僱儖儞僗僩偺幃偱梌偊傜傟傞丅
丂丂丂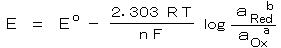 丂丂丂丂丂丂丂丂丂丂丂丂丂丒丒丒丒丒丂乮侾乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丒丒丒丒丒丂乮侾乯
丂丂偨偩偟丄丂俤倧 丗 昗弨巁壔娨尦揹埵丄 俿丗 愨懳壏搙丄 値丗 斀墳偵娭梌偡傞揹巕悢丄 俥丗
僼傽儔僨乕掕悢乮俋俇係俉俆 俠/倣倧倢乯
丂丂乮仏丂乭昗弨乭偲偼丄俀俆亷丄梟塼 侾俵 偁傞偄偼 婥懱 侾倐倎倰 偵偍偗傞偺堄乯
丂丂妶検學悢亖侾 偵嬤帡偱偒丄壏搙偑俀俆亷偺応崌偼丄丂丂丂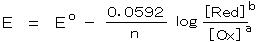 丂丂丂丂丂丂丒丒丒丒丒丂乮俀乯
丂丂丂丂丂丂丒丒丒丒丒丂乮俀乯
偱偁傝丄倢倧倗 偺拞枴偼 儌儖暯峵掕悢偺敿暘偲側偭偰偄傞丅屌懱乮嬥懏丒扨懱側偳乯傗 塼懱乮俫2俷側偳乯偺弮暔幙偼 扨埵妶検偲偡傞丅
僱儖儞僗僩偺幃傛傝丄俤 偼丄昗弨揹埵 俤倧 偐傜偺 擹搙僶儔儞僗偵傛傞揹埵偺偢傟偲側傞丅
丂丂仏丂偙傟傜偺昗弨巁壔娨尦揹埵偼丄僱儖儞僗僩偺採埬偵傛傝丄悈慺揹嬌偺揹埵乮俶俫俤 偲棯婰丗丂俀 俫亄 亄 俀 倕亅 亖 俫2丄丂俹倲乥俫2丄俫亄乥丄偨偩偟丄埑椡 侾倐倎倰丄壏搙俀俆亷乯傪 侽 倁 偲抲偒丄偦傟偧傟悈慺揹嬌偵懳偡傞揹埵嵎偲偟偰掕媊偝傟偰偄傞丅
丂丂丒丂堎側傞俀偮偺敿揹抮傪慻傒崌傢偣偰 揹埵嵎傪惗偠偝偣丄僈儖僶僯揹抮傪峔惉偡傞偙偲偑偱偒傞丅
丂丂偨偲偊偽丄摵傪 侾俵棸巁摵梟塼偵丄垷墧傪 侾俵棸巁垷墧梟塼偵丄偦傟偧傟捫偗偨俀偮偺敿揹抮傪丄墫嫶乮拞偺揹夝幙僀僆儞偑摫懱偵側傞乯偱偮側偖偲丄摵斅偵
+ 丄垷墧斅偵 亅偺揹埑偑婲偙傝丄僈儖僶僯揹抮乮僟僯僄儖揹抮乯偑偱偒傞丅丂奺
敿揹抮偺敿斀墳偲丂昗弨巁壔娨尦揹埵偼丄丂俠倳2亄 亄 俀 倕亅 亖 俠倳丗丂侽丏俁俁俈倁丄丂丂倅値2亄 亄 俀倕亅 亖 倅値丗丂亅侽丏俈俇俁倁丂側偺偱丄
慡懱偺揹抮峔惉偲 揹埵嵎乮亖僈儖僶僯揹抮偺揹埑乯偼丄
丂丂丂丂丂丂丂丂丂丂俠倳乥俠倳2亄乮侾俵乯乥乥倅値2亄乮侾俵乯乥倅値丄丂丂丂丂俤們倕倢倢 亖 侽丏俁俁俈 亅 乮亅侽丏俈俇俁乯 亖 侾丏侾侽侽倁丂丂丂偲側傞丅
丂丂丒丂摨條偵丄乭梟塼乭偺巁壔娨尦斀墳偵傛傞敿揹抮偺慻傒崌傢偣偵傛偭偰傕丄僈儖僶僯揹抮傪峔惉偡傞偙偲偑偱偒傞丅
丂丂偨偲偊偽丄丂俥倕3亄偲 俥倕2亄 丄俬3亅 偲 俬亅 偺偦傟偧傟偺崿崌梟塼傪墫嫶偱偮側偓丄偦傟偧傟偺梟塼偐傜敀嬥偱揹嬌傪庢傝弌偟偨僈儖僶僯揹抮偼丄揹嬌偺昞柺嬤朤偱偦傟偧傟巁壔覍硵紨綁瀭獘N偙傝丄
丂丂丂俥倕3亄 亄 倕亅 亖 俥倕2亄 丄丂俤倧 乮俥倕3亄/ 俥倕2亄乯 亖 侽丏俈俈侾倁丄丂丂丂俬3亅 亄 俀 倕亅 亖 俁 俬亅 丄丂俤倧 乮俬3亅/ 俬亅乯 亖 侽丏俆俁俇倁丂
側偺偱丄 揹抮揹埑偼 僱儖儞僗僩偺幃乮俀乯傛傝丄
丂丂丂 俤們倕倢倢丂亖丂俤乮俥倕3亄/ 俥倕2亄乯 亅 俤乮俬3亅/ 俬亅乯
丂丂丂丂丂丂丂丂亖丂{ 俤倧 乮俥倕3亄/ 俥倕2亄乯 亅 侽丏侽俆俋俀 倢倧倗乮乵俥倕2亄乶/乵俥倕3亄乶乯}丂亅丂{ 俤倧 乮俬3亅/ 俬亅乯 亅 乮侽丏侽俆俋俀 /俀乯 倢倧倗乮乵 俬亅乶/乵俬3亅乶乯}丂
丂丂丂丂丂丂丂丂亖丂( 俤倧 乮俥倕3亄/ 俥倕2亄乯 亅 俤倧 乮俬3亅/ 俬亅乯乯丂亅丂乮侽丏侽俆俋俀 /俀乯 倢倧倗乮乵俥倕2亄乶2乵俬3亅乶/乵俥倕3亄乶2乵 俬亅乶3乯
丂丂丂丂丂丂丂丂亖丂( 俤倧 乮俥倕3亄/ 俥倕2亄乯 亅 俤倧 乮俬3亅/ 俬亅乯乯丂亅丂乮侽丏侽俆俋俀 /俀乯 倢倧倗 俲
丂丂偙偺揹抮斀墳偑暯峵偵払偟偨偲偒丄丂俤們倕倢倢 亖 侽丂丂偩偐傜丄
丂丂丂 俤倧們倕倢倢 亖 俤倧們倎倲倛倧倓倕 亅 俤倧倎値倧倓倕 丂亖丂 俤倧 乮俥倕3亄/ 俥倕2亄乯 亅 俤倧 乮俬3亅/ 俬亅乯丂亖丂乮侽丏侽俆俋俀 /俀乯 倢倧倗 俲
偲側傝丄
丂丂慡斀墳乮巁壔娨尦斀墳乯丂丂俀 俥倕3亄 亄 俁 俬亅 亖 俀 俥倕2亄 亄 俬3亅 丂偵偮偄偰丄傑偨丄堦斒揑偵丄
丂丂丂丂丂丂丂丂丂丂丂倢倧倗 俲丂亖丂値 乮俤倧們倎倲倛倧倓倕 亅 俤倧倎値倧倓倕乯/侽丏侽俆俋俀丂丂丂丂丂丂丂丂丂丂丒丒丒丒丒丒丂乮俁乯
丂丂偟偨偑偭偰丄昗弨巁壔娨尦揹埵偑傢偐傟偽丄俀俆亷偵偍偗傞 巁壔娨尦斀墳偺 暯峵掕悢 俲 偑寁嶼偱偒傞丅
丂丂傑偨丄丂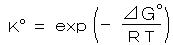 丂傛傝丄
丂傛傝丄
丂丂僊僽僘偺昗弨惗惉帺桼僄僱儖僊乕嚈俧倧乮俰/倣倧倢乯偑丄丂丂嚈俧倧丂亖丂亅 値 俥 俤倧們倕倢倢丂丂丒丒丒丒丂乮係乯
偺傛偆偵昞偝傟傞丅 俥丗 僼傽儔僨乕掕悢乮俋俇係俉俆 俠/倣倧倢乯
丂丂偙偺乮係乯幃偼丄昗弨忬懺偺僈儖僶僯揹抮偑帺敪揑偵曻揹偡傞揹椡偑 偦偺傑傑 昗弨惗惉帺桼僄僱儖僊乕偱偁傞偙偲傪昞偟丄嚈俧倧 偑 乭斀墳偺嬱摦椡乭偱偁傞偙偲偺 偒傢傔偰捈愙揑側昞尰偵側偭偰偄傞丅乮媡偵丄奜晹偐傜揹椡傪梌偊偰揹夝偡傟偽丄偦偺僄僱儖僊乕偺暘偩偗暔幙偑惗惉偡傞偙偲傪傕昞傢偟偰偄傞丅乯
丂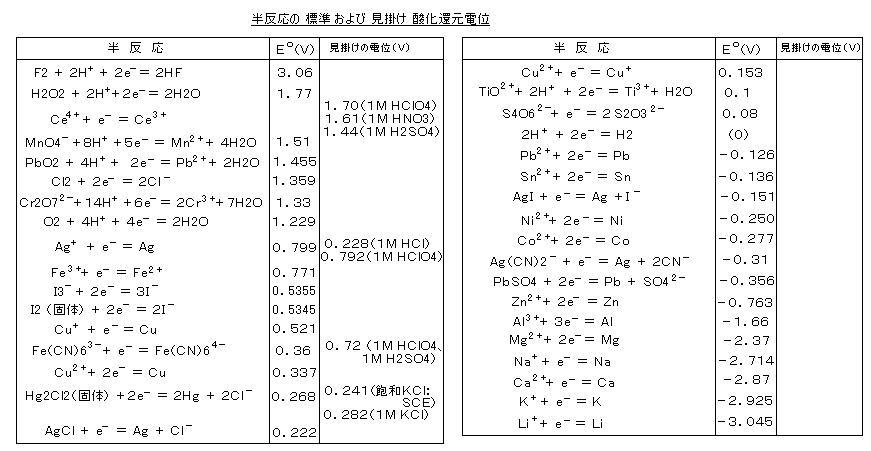
丂丂俀丏丂僈儖僶僯揹抮偺應掕幚尡
丂丂乮侾乯丂崅擖椡僀儞僺乕僟儞僗 倣倁寁 偺嶌惢丗
丂丂嶲徠揹嬌傗巜帵揹嬌偵懳偟丄揹埑崀壓側偟偵旝庛側揹棳偺揹埑傪應掕偡傞昁梫偑偁傞偺偱丄僨僕僞儖僥僗僞乕傛傝傕崅僀儞僺乕僟儞僗偺丄愱梡偺
倣倁寁傪嶌惢偟偨丅
丂丂乮仏丂晛捠偼丄乭揹埵嵎寁乮億僥儞僔僆儊乕僞乯乭傗億僥儞僔儑僗僞僢僩梡偺愱梡婡婍傪梡偄傞丅丂丒丒丒丂僒僀僋儕僢僋儃儖僞儞儊僩儕乕乮俠倁乯乯
丂丂巗斕偺乭僨僕僞儖倣倁揹埑寁僉僢僩乮廐寧揹巕乯乭乮 倣倎倶 俀侽侽丏侽倣倁丄擖椡僀儞僺乕僟儞僗丗應掕晄壜丒悇掕侾侽俧兌丄擖椡僶僀傾僗揹棳丗侾倫俙乯偵丄擖椡僀儞僺乕僟儞僗偑侾侾侾俵兌掱搙偵側傞傾僢僥僱乕僞乕乮侾侽侽俵兌丗 侾侽俵兌亄侾俵兌亄侾侽侽倠兌乯傪晅偗偰丄倣倎倶
俀丏侽侽侽倁昞帵愱梡偲偟偨丅丂挷惍売強偼僗働乕儖愝掕梡億僥儞僔儑儊乕僞乮侾侽倠兌乯偺侾売強偩偗偱偁傝丄儕僯傾儕僥傿乕乮捈慄惈乯偼撪憼偺俴俽俬乮俬俠俴俈侾俁俇俹俴乯偺惈擻偵傛傞丅
丂丂妑惓偼丄僨僕僞儖僥僗僞乕偱揹埑偑應掕偱偒傞傎偳揹棳梕検偺戝偒偄僟僯僄儖揹抮乮侾丏侾侽侽倁丄 倅値乥侾俵 倅値俽俷4乥乥侾俵 俠倳俽俷4乥俠倳 乮俠倳俽俷4丒丒丒傎偲傫偳朞榓乯乯傪丄怴婯偵挷惢偟偰峴側偭偨丅乮婓棸巁傪奺梟塼偵悢揌壛偊傞乯丂奺梟塼娫偼墫嫶乮偊傫偒傚偆丟 侾俵 俲俠倢悈梟塼偵姦揤乮偐側傝峝傔乯傪梟偐偟丄倀帤偵嬋偘偨冇侾侽倣倣偺僈儔僗娗偵廩揢偟偨傕偺乯偱偮側偘偨丅
丂丂 倅値亅俠倳娫偺應掕抣偼丄 僨僕僞儖僥僗僞乕乮怴偟偄侽侽俇俹揹抮巊梡乯偲暲楍偵偟偰應傝丄倣倁寁偺偼僗働乕儖愝掕偺億僥儞僔儑儊乕僞傪挷惍偟偨丅乮仏丂僟僯僄儖揹抮偼丄壗夞偐巊梡偡傞偲揹埑偑壓偑偭偰偔傞偺偱拲堄乯
丂丂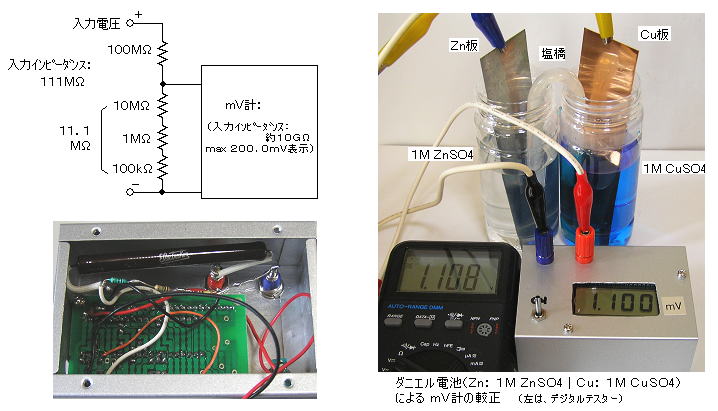
丂丂乮俀乯丂僇儘儊儖嶲徠揹嬌偵傛傞 敿揹抮揹埵偺應掕丗
丂丂朞榓僇儘儊儖嶲徠揹嬌乮俽俠俤 偲棯婰丄 俫倗2俠倢2乮乮亖墫壔戞堦悈嬧丄娒焽乮偐傫偙偆乯丄僇儘儊儖乯 偺屌懱乯 亄 俀倕- 亖 俀俫倗 亄 俀俠倢-丄 俫倗乥俫倗2俠倢2乥俠倢-乥倝値 朞榓 俲俠倢丗 侽丏俀係侾倁乯傪梡偄偰丄丂侾乯 僟僯僄儖揹抮偺奺敿揹抮丄 俀乯 俥倕3亄/ 俥倕2亄乮棸巁揝乮嘦乯偲墫壔揝乮嘨乯 奺侾俵 倝値 侾俵 俫俶俷3乯丄 俠倕4亄/俠倕3亄 乮棸巁僙儕僂儉乮嘨乯偲棸巁僙儕僂儉乮嘩乯 奺侽丏俀俵 倝値 侾俵 俫俶俷3乯偺奺敿揹抮丄偺揹埵傪應掕偡傞丅 僱儖儞僗僩幃乮侾偺乮俀乯乯偵傛傟偽丄偡傋偰僀僆儞偵夝棧偟偰偄傟偽丄梟塼偺僀僆儞擹搙偺嵎偑柍偔 幃偺 倢倧倗 撪偼 侾 偵側傝丄 俤 佮 俤倧 偵側傞偼偢偱偁傞丅
丂丂寢壥偼丄應掕揹埑偑曄摦偡傞偙偲偼側偔丄偙偺擖椡僀儞僺乕僟儞僗侾侽侽俵兌偺 倣倁寁偱廩暘埨掕偟偰偄偨丅乮僨僕僞儖僥僗僞乕偱偼戝偒偔曄摦偡傞乯丂偟偐偟丄慡懱揑偵 俽俠俤偺揹埑偑亄懁偵栺俀侽倣倁僔僼僩偟丄俽俠俤撪晹偱暃斀墳偑婲偙偭偰偄傞壜擻惈偑偁傝丄傑偨丄偙傟偱傕傑偩倣倁寁偺擖椡僀儞僺乕僟儞僗偑掅偄偲巚傢傟偨丅丂傑偨丄梟塼宯偺
俥倕 偱栺俇俆倣倁乮幚幙係俆倣倁乯傕揹埑崀壓偟偨丅 乮俠倕 偼丄侾俵 倝値
俫俶俷3偺揹埑偑尒妡偗偺抣偱偁傝丄偢傟偰摉慠乯
丂丂傑偨丄巜帵揹嬌乮仏 揹嬌昞柺偱婲偙傞僀僆儞偺巁壔娨尦斀墳偵傛傞揹埑傪廍偆乯偵梡偄偨 弮崟墧朹乮俋俋丏俋俋亾乯偲敀嬥慄僜儗僲僀僪乮冇侽丏俆倣倣俹倲慄
栺俁侽們倣暘傪姫偄偨傕偺乯偺應掕揹埑偼丄偙傟傜偺擹搙偱偼揹埑偵傎偲傫偳嵎偑柍偐偭偨丅
|
僟僯僄儖揹抮丗俠倳亅倅値慡揹埑 |
丂丂倅値丂倴倱丏俽俠俤丂 |
丂丂俠倳丂倴倱丏俽俠俤丂 |
丂俥倕3亄/ 俥倕2亄 倴倱丏俽俠俤丂 |
丂俠倕4亄/俠倕3亄 倴倱丏俽俠俤 |
丂丂寁嶼抣
乮100亾夝棧偲偡傞乯 |
丂侽丏俈俇俁亄侽丏俁俁俈亖
丂丂丂丂丂侾丏侾侽侽倁 |
丂侽丏俈俇俁亄侽丏俀係侾亖
丂丂丂丂侾丏侽侽係 |
丂侽丏俁俁俈亅侽丏俀係侾亖
丂丂丂丂侽丏侽俋俇 |
丂侽丏俈俈侾亅侽丏俀係侾亖
丂丂 丂丂侽丏俆俁侽 |
乮俠倕僀僆儞偑奺侾俵偺応崌丄
侾丏俇侾侽亅侽丏俀係侾亖丂侾丏俁俇俋丂乯 |
| 丂丂應掕抣 |
丂丂丂丂丂侾丏侾侽侽倁 |
丂丂丂丂侾丏侽俀俀 |
丂丂丂丂侽丏侽俈俆 |
丂丂 丂丂侽丏係俇俆 |
丂丂丂丂丂侾丏俀俁係 |
| 丂丂丂曃嵎 |
丂丂丂丂丂侽丏侽侽侽倁 |
丂丂丂亄侽丏侽侾俉 |
丂丂丂亅侽丏侽俀侾 |
丂丂丂亅侽丏侽俇俆 |
丂丂丂乮亅侽丏侾俁俆乯丂 |
丂丂仏丂倣倁寁偺 傾僢僥僱乕僞乕偺掞峈傪 侾俧兌 丗 侾侾侾俵兌 乮擖椡僀儞僺乕僟儞僗亖侾丏侾侾俧兌乯偵曄偊傞偲丄揹埑昞帵抣偑埨掕偡傞偺偵帪娫偑偐偐傝丄應掕抣傕丄俥倕丗
侽丏係俈侽倁丄 俠倕丗 侾丏俀係係倁 倴倱丏 俽俠俤 偱 偦傟傎偳戝偒偔忋徃偟側偐偭偨偺偱丄俴俽俬偺惈擻偲偺寭偹崌偄偱俀侽侽俵乣俁侽侽俵兌偑倐倕倱倲偐偲巚傢傟傞丅

丂丂師偵丄 俥倕3亄/ 俥倕2亄 偺擹搙斾傪曄峏偟偰應掕偟偨丅乮俥倕3亄/ 俥倕2亄 亖 侽丏俆俵/侽丏俆俵丄 侽丏俀俆俵/侽丏俀俆俵丄 侾俵/侽丏俀俆俵丄 侽丏俀俆俵/侾俵
丂倴倱丏俽俠俤 丄 偡傋偰 倝値 侾俵 俫俶俷3丄巜帵揹嬌丒敀嬥僐僀儖乯
丂丂僱儖儞僗僩幃乮乮俀乯幃乯傛傝丄嵟弶偺俁偮偼 倢倧倗 撪偑侾偱偁傝 俤 亖
俤倧 乮俥倕3亄/ 俥倕2亄乯 亅 侽 亖 侽丏俈俈侾倁丂偱偁傝丄 巆傝偺俀偮偼丄乵俥倕2亄乶/乵俥倕3亄乶 偑偦傟偧傟 侾/係丄 係 偱偁傝丄丂俤 亖 侽丏俈俈侾 亅 侽丏侽俆俋俀 倢倧倗
乮侾/係乯 亖侽丏俉侽俈倁丄丂 俤 亖 侽丏俈俈侾 亅 侽丏侽俆俋俀 倢倧倗 係
亖 侽丏俈俁俆倁丂偲側傞偼偢偱偁傞丅
丂丂寢壥偼丄忋偲摨偠傛偆側曃嵎偑惗偠偨偑 傎傏堦掕偱偁傝丄偙傟傪廋惓偡傞偲丄僱儖儞僗僩偺幃偺捠傝丄擹搙斾 乵俥倕2亄乶/乵俥倕3亄乶 偵傛偭偰揹埵偑曄壔偡傞偺偑妋擣偱偒偨丅丂乵俥倕2亄乶/乵俥倕3亄乶亖侾 偺偲偒偼丄侾俵 傕 侽丏俀俆俵 傕 傎傏摨偠偱偁傝丄寢峔掅偄擹搙傑偱偙偺倣倁寁偱應掕偱偒傞偙偲偑暘偐偭偨丅乮侽丏侾俵傑偱摨條偺揹埑偵應傟傞偑丄侽丏侽侾俵埲壓偵側傞偲媫偵嫸偆乯
|
侾俵 俥倕3亄/ 侾俵 俥倕2亄 |
侽丏俆俵 俥倕3亄/侽丏俆俵 俥倕2亄 |
侽丏俀俆俵俥倕3亄/侽丏俀俆俵俥倕2亄 |
侾俵 俥倕3亄/侽丏俀俆俵俥倕2亄 |
侽丏俀俆俵俥倕3亄/侾俵 俥倕2亄 |
| 寁嶼抣 |
丂侽丏俈俈侾亅侽丏俀係侾亖
丂丂丂丂侽丏俆俁侽倁 |
丂丂侽丏俈俈侾亅侽丏俀係侾亖
丂丂丂丂丂丂侽丏俆俁侽 |
丂丂侽丏俈俈侾亅侽丏俀係侾亖
丂丂丂丂丂丂侽丏俆俁侽 |
丂丂侽丏俉侽俈亅侽丏俀係侾亖
丂丂丂丂丂侽丏俆俇俇 |
丂丂侽丏俈俁俆亅侽丏俀係侾亖
丂丂丂丂丂侽丏係俋係 |
| 應掕抣 |
丂丂丂丂侽丏係俇係倁 |
丂丂丂丂丂丂侽丏係俇俆 |
丂丂丂丂丂丂侽丏係俇俉 |
丂丂丂丂丂侽丏係俋俆 |
丂丂丂丂丂侽丏係侾俉 |
| 丂曃嵎 |
丂丂 亅侽丏侽俇俇倁 |
丂丂丂丂丂亅侽丏侽俇俆 |
丂丂丂丂丂亅侽丏侽俇俀 |
丂丂丂丂亅侽丏侽俈侾 |
丂丂丂丂亅侽丏侽俈俇 |
丂丂乮俁乯丂嬧-墫壔嬧揹嬌偺嶌惢幚尡丗
丂丂婎弨揹埵傪嶌傞敿揹抮偵偼丄悈慺揹嬌乮俀俫+ 亄 俀倕- 亖 俫2丄俹倲乮敀嬥崟揹嬌乯乥俫2丄俫+乥丗 侽丏侽侽乮倁乯乯丄朞榓僇儘儊儖揹嬌乮俫倗2俠倢2 亄 俀倕- 亖 俀俫倗 亄 俀俠倢-丄俫倗乥俫倗2俠倢2乥俠倢-乥丗 侽丏俀係侾乮倁乯乯偑偁傞偑丄偙偙偱偼嶌傝傗偡偄 嬧-墫壔嬧揹嬌乮俙倗俠倢 亄 倕- 亖 俙倗 亄 俠倢-丄 俙倗乥俙倗俠倢乥俠倢-乥丄侽丏俀俀俀倁丄倝値 侾俵 俲俠倢丄俀俆亷乯傪嶌惢偟偰丄僟僯僄儖揹抮偺敿揹抮揹埵傪應掕偟偨丅
墫壔嬧偼嬧慄乮冇侽丏俉倣倣乯傪梲嬌偲偟偰栺侾侽亾俫俠倢 偱揹夝偟偰晅拝偝偣丄侾俵
俲俠倢偵怹偟丄侾俵 俲俠倢姦揤偱壓晹傪晻偠偨冇侾俆倣倣僈儔僗娗拞偵曐帩偟偨丅乮曐懚塼偼
摍挘偺侾俵 俲俠倢乯
丂丂寢壥偼丄擖椡僀儞僺乕僟儞僗偑傎偲傫偳栤戣偲側傜側偄僟僯僄儖揹抮偺應掕偱偐側傝偺偢傟偑偁傝丄俙倗/俙倗俠倢揹嬌偼丄朞榓僇儘儊儖揹嬌偺応崌偲摨條偵丄
侽丏俀俆俈亅侽丏俀俀俀 亖 侽丏侽俁俆倁傎偳 亄懁偵僔僼僩偟偨丅
丂丂丂丂丂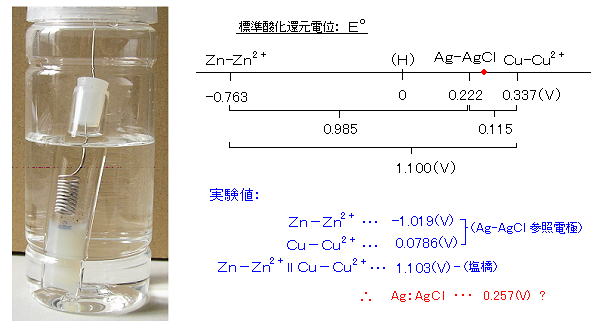
丂丂俁丏丂巁壔娨尦揌掕
丂丂悈梟塼撪偱丄僈儖僶僯揹抮偺暯峵掕悢偑廩暘戝偒偔丄斀墳懍搙偑懍偄応崌 揌掕偵梡偄傞偙偲偑偱偒傞丅 揌掕偺応崌偼丄悈梟塼撪偱揹抮斀墳乮巁壔娨尦斀墳乯偑姰寢偟偰偄傞偺偱丄偙偙偱偼揹埵嵎傪應掕偡傞昁梫偼柍偄丅 傛偔抦傜傟偰偄傞巁壔揌掕朄偲偟偰丄夁儅儞僈儞巁僇儕僂儉朄丄廳僋儘儉巁乮擇僋儘儉巁乯僇儕僂儉朄丄棸巁僙儕僂儉乮嘩乯朄丄傑偨丄娨尦揌掕朄偲偟偰丄儓僂慺娨尦朄側偳偑偁傞丅
丂丂丒丂儓僂慺娨尦朄丗丂丂儓僂慺巁壔揌掕朄偼斀墳懍搙偑抶偄偺偱偁傑傝梡偄傜傟側偄偑丄僠僆棸巁僫僩儕僂儉乮娨尦嵻乯偵傛傞 儓僂慺偺媡揌掕偼傛偔梡偄傜傟傞丅
丂丂儓僂慺乮俬2丗 悈梟塼拞偱 俬3亅乯偍傛傃 僠僆棸巁僫僩儕僂儉乮俶倎2俽2俷3乯偺 奺 敿斀墳偼丄
丂丂丂丂丂丂俬3亅 亄 俀 倕亅 亖 俁 俬亅 丄丂俤倧 乮俬3亅/ 俬亅乯 亖 侽丏俆俁俇倁
丂丂丂丂丂丂俀 俽2俷32亅 亖 俽4俷62亅乮巐僠僆儞巁僀僆儞乯 亄 俀 倕亅 丄丂俤倧 乮俽4俷62亅/俽2俷32亅乯 亖 侽丏侽侽俉倁
丂丂偟偨偑偭偰丄揌掕斀墳偼丄
丂丂丂丂丂丂俬2 亄 俀 俽2俷32亅 亖 俀 俬亅 亄 俽4俷62亅 丄丂丂俤倧們倕倢倢 亖 侽丏俆俀俉倁
丂丂侾偺乮俁乯幃傛傝丄丂倢倧倗 俲 亖 侾俈丏俉 乮値亖俀乯丄丂 俲 亖 俇丏俁侾亊侾侽17丂丂偱偁傝丄斀墳偼傎偲傫偳姰慡偵塃偵恑傒 偙偺斀墳偼揌掕岦偒偱偁傞丅丂傑偨丄侾偺乮係乯幃傛傝丂嚈俧倧丂亖丂亅侾丏侽俀亊侾侽5俰/倣倧倢丂偱乮晧偺曽岦偵乯偐側傝戝偒偄丅
丂丂丒丂僂傿儞僋儔乕朄偵傛傞 悈摴悈偺梟懚巁慺偺揌掕丗丂丂僶働僣偵擖傟偰 敿擔 媯傒抲偄偨悈摴悈拞偺梟懚巁慺検傪挷傋偨丅悈摴悈拞偺梀棧墫慺偼丄悈偲斀墳偟偰梀棧巁慺偵曄傢傞丅乮嬥嫑偑廩暘惗偒傞傎偳丄堄奜偲巁慺偑梟偗崬傫偱偄傞両乯丂偨傔偟偵丄婥朅偑擖傜側偄傛偆偵奧傪偟偨廤婥價儞偵偼丄巁慺傜偟偄婥朅偑敪惗偟偰偄偨丅乮悈壏栺侾侽亷乯
丂丂嶌嬈偱拲堄偡傋偒揰偼丄巁慺偑屌掕偝傟傞傑偱偼嬻婥偵怗傟偝偣側偄偙偲偱丄婥朅偑擖偭偨応崌偼丄偡傒傗偐偵悈傪懌偟偰婥朅傪捛偄弌偟丄廤婥價儞偺奧傪僗儔僀僪偝偣傞丅乮愱梡偺乭巁慺價儞乮捠忢侾侽侽倣倢乯乭偼丄愷偺悹傝崌傢偣晹暘偑幬傔偵愗偭偰偁傞乯
丂丂揌掕偼丄巁慺偑屌掕偝傟儓僂慺偑惗惉偟偨塼 侾侽侽倣倢傪庢傝丄侽丏侽侾俵
俶倎2俽2俷3 傪揌壓偟偰峴側偆偑丄巜帵栻偺僨儞僾儞塼乮壜梟惈僨儞僾儞巊梡乯偼丄儓僂慺偺怓偑廩暘敄偔側偭偰偐傜揧壛偡傞丅乮儓僂慺偺僨儞僾儞嶖懱偺斀墳偑抶偄偨傔乯丂廔揰捈慜偱偼丄侾揌壛偊傞偛偲偵悢暘偐偗丄僗僞乕儔乕偱廩暘潣漚偟側偑傜峴側偆丅廔揰偼丄惵怓偑姰慡偵徚偊偨抧揰丅
丂丂巁慺偺屌掕斀墳偼丄丂丂俵値2亄 亄 俀 俷俫亅 仺 俵値乮俷俫乯2伀 丄丂俷2 亄 俀 俵値乮俷俫乯2 仺 俀 俵値俷乮俷俫乯2丂乮僆僉僔悈巁壔儅儞僈儞乮嘩乯乯
丂丂巁傪壛偊偨偲偒偺儓僂慺惗惉偼丄丂丂俵値俷乮俷俫乯2 亄 俀 俬亅 亄 係 俫亄 仺 俵値2亄 亄 俬2 亄 俁 俫2俷
丂丂亪丂斀墳儌儖斾偼丄丂丂俷2 丗 俵値俷乮俷俫乯2 亖 侾丗俀丄丂俵値俷乮俷俫乯2丂丗 俬2 亖 侾丗侾丄丂俬2 丗 俽2俷32亅 亖 侾丗俀丂傛傝丄丂俷2 丗 俽2俷32亅 亖 侾丗係
丂丂寢壥偼丄侾侽侽倣倢偵懳偟偰丄侽丏侽侾俵 俶倎2俽2俷3 傪 侾俀丏侾係倣倢徚旓偟偨丅丂巁慺擹搙偼丄侾丗係 亖 倶俵 亊 侾侽侽倣倢 丗 侽丏侽侾俵 亊 侾俀丏侾係倣倢丂傛傝丄倶 亖 俁丏侽係亊侾侽亅4俵
丂丂亪丂倣倗/倢 偲偟偰偼丄丂俁丏侽係亊侾侽亅4亊俁俀丏侽亊侾侽侽侽 亖 俋丏俈俁 俷2倣倗/倢
丂丂悈壏侾侽亷偲偟偰偺朞榓巁慺擹搙偺僨乕僞偼棟壢擭昞偵傕柍偐偭偨偑丄侽亷偱
侾俁丏俋俈倣倗/倢丄俀侽亷偱 俉丏俉係倣倗/倢丄 係侽亷偱 俇丏俆俇倣倗/倢
傪撪暘丒悇掕偟偰丄侾侽亷偱 侾侽丏侾倣倗/倢 偲偟偰丄
丂丂亪丂巁慺偺朞榓搙乮俢俷乯亾偼丄丂乮俋丏俈俁/侾侽丏侾乯亊侾侽侽 亖 俋俇 亾丂偱偁傝丄傎偲傫偳朞榓偵嬤偐偭偨丅丂乮們倖丏 塰梴晉壔偑恑傫偩屛悈偱偼丂俇侽亾偔傜偄乯
丂丂
丂丂丂乮嶲峫乯丂壏搙偑曄壔偡傞応崌偺 惗惉帺桼僄僱儖僊乕慄恾乮僄儕儞僈儉慄恾乯偺撉傒曽丗
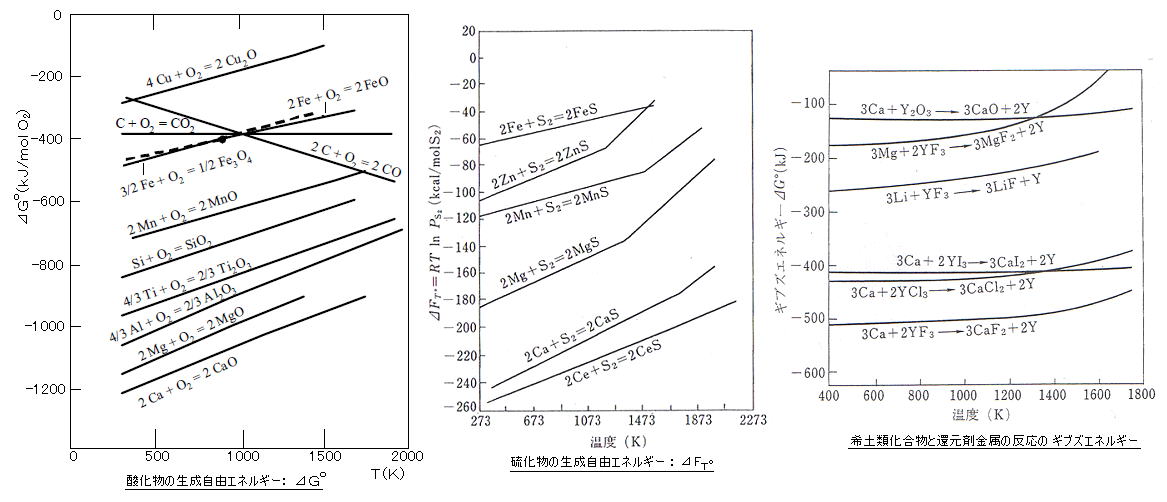
丂丂嘆丂巁壔暔偺惗惉帺桼僄僱儖僊乕丗丂丂惢揝偵偍偄偰丄崅楩忋晹乮俆侽侽乣俉侽侽亷乯偱偼丄丂俥倕2俷3
亄 俁俠俷 仺 俀俥倕 亄 俁俠俷2丂丒丒丒丂俠俷 偵傛傞娨尦丄丂崅楩壓晹乮俋侽侽乣侾俀侽侽亷乯偱偼丄丂丂俥倕2俷3
亄 俁俠 仺 俀俥倕 亄 俁俠俷丂丒丒丒丂俠 偵傛傞捈愙娨尦丄丂偑婲偙傞丅
丂丂扽慺偺巁壔斀墳偵拲栚偡傞偲丄丂侾乯丂俠 亄 俷2 仺 俠俷2 乮掅壏堟乯丗 嚈俧亖亅俋係丏俁倠們倎倢丄嚈俫亖亅俋係丏侾倠們倎倢丄嚈俽亖亄侽丏俈侽丂丂俀乯丂俀俠 亄 俷2 仺 俀俠俷 乮崅壏堟乯丗 嚈俧亖亅俇俆丏俇倠們倎倢丄嚈俫亖亅俆俀丏俉倠們倎倢丄嚈俽亖亄係俀丏俉俉丂偱偁傝丄侾乯 偺婥懱儌儖悢偺曄壔偑 侾儌儖仺侾儌儖 偱偁傞偺偵懳偟丄俀乯 偼 侾儌儖仺俀儌儖 偱憹壛偟丄棎嶨偝偑憹壛偡傞偺偱丄偙偺傛偆偵
僄儞僩儘僺乕曄壔嚈俽偑戝偒偄丅忋恾嵍偺丄扽慺偺擱從斀墳偵偮偄偰偺 嚈俧 亖 嚈俫 亅 俿嚈俽丂偺慄恾偼丄偦偺岡攝 倓乮嚈俧乯/倓俿亖亅嚈俽 偑丄 掅壏堟偱偼傎偲傫偳悈暯偱偁傝丄崅壏堟偱偼塃壓偑傝偵側傝丄椉捈慄偼栺俋俈俋倠乮俈侽俇亷乯偱岎嵎偡傞丅
丂丂偟偨偑偭偰丄丂俠 亄 俠俷2 仺 俀俠俷丂偺斀墳偼丄俈侽俇亷埲忋偺崅壏偱恑傓丅
俈侽俇亷偵偍偗傞暯峵掕悢偼丄 俲倫 亖 乮俹俠俷乯2/俹俠俷2 亖 侾丅
丂丂堦曽丄崅楩壓晹偐傜擬晽傪悂偒崬傫偱巁慺夁忚偵側偭偰傕丄丂俀俠俷 亄 俷2
仺 俀俠俷2丂偺斀墳偼丄婥懱 俁儌儖仺俀儌儖 乮嚈俧亖亅侾侾侽丏俇倠們倎倢丄嚈俫亖亅侾俀俁丏侽倠們倎倢丄嚈俽亖侽丏俈侽亊俀亅係俀丏俉俉亖亅係侾丏係俉
乯偺傛偆偵 僄儞僩儘僺乕偑尭彮偡傞斀墳側偺偱丄崅壏傎偳婲偙傝偵偔偔側傝 壓晹偱偼
俠俷 偺傒偲側傞丅
丂丂嘇丂棸壔暔偺惗惉帺桼僄僱儖僊乕丗丂丂峾拞偺棸墿壔崌暔乮摿偵丄俵値俽宆夘嵼暔乯偼丄擬娫壛岺帪偵墑怢偟偰墑惈攋夡傗悈慺桿婲妱傟偺廳戝側栤戣傪堷偒婲偙偡丅偦偙偱丄惢峾抜奒偱棸墿検傪尭彮偝偣丄俵値俽傪墑怢偟偵偔偄媴忬偵偡傞偨傔偵丄棸墿偲偺寢崌椡偑 俵倗丄俠倎傛傝傕嫮偄 儈僢僔儏儊僞儖乮俠倕偑庡惉暘乯傪揧壛偡傞丅
丂丂嘊丂婓搚椶嬥懏偺惛楤丗丂婓搚椶壔崌暔乮俁壙埲忋乯偺偆偪丄僼僢壔婓搚椶傪
俠倎 偱娨尦偡傞応崌丄嚈俧 偑乮晧偺曽岦偵乯嵟傕戝偒偔 斀墳偑梕堈偵恑峴偡傞丅乮偨偩偟丄俀壙偺俽倣乮幌爻褋j丄俤倳乮瞻鬯叱褋j丄俿倣乮仑逞乯丄倄倐乮帛觅宿逞乯偼偙偺曽朄偱偼斀墳偑恑峴偣偢丄俽倣側偳偺忲婥埑偑掅偄偙偲傪棙梡偟偰
儈僢僔儏儊僞儖傪娨尦嵻偲偟偰宯奜傊忲棷偟偰惢憿偡傞乯
丂丂丒丂俠倳俽丄俶倝俽丄俹倐俽 側偳偼丄惛峼傪 扽慺暘傪慡偔梡偄偢丄悂偒崬傓嬻婥乮俷2乯検傪挷愡偡傞偩偗偱壏搙偲巁慺暘埑偺僐儞僩儘乕儖傪峴偄丄嶳尦側偳偱
捈愙 慹儊僞儖傪惢憿偡傞丅乮儅僢僩梠楤乯丂丂倅値俽 偼偙偺曽朄偱偼柍棟偱丄堦搙 惛峼傪巁壔鄤從偟偰 倅値俷 偲偟偰偐傜丄僐乕僋僗偲擬偟偰忲棷偡傞丅
丂丂丂丂丂丂丂仒丂丂嚈俧倧 偲 僄儞僩儘僺乕偵偮偄偰丗
丂丂暔棟壔妛揑偵尒傞偲丄壔妛偼丄侾丏暯峵榑 偲 俀丏斀墳懍搙榑 偵戝暿偝傟丄斀墳懍搙榑傕暯峵榑傪儀乕僗偲偟偰偄傑偡丅堦尒娭學柍偄條偵尒偊傞擬椡妛偲壔妛暯峵榑偱偡偑丄屆揟暔棟偺擬椡妛偐傜偡傋偰摫偐傟傑偡丅
丂丂俧乮僊僽僘偺帺桼僄僱儖僊乕乯傪丄 俧 佭 倀亄俹倁亅俿俽 乮亖 俫亅俿俽乯 偲掕媊偡傞偲丄暯峵忬懺乮亖偄傢偽丄廩暘乭巰傫偩乭丄乭儕儔僢僋僗偟偨乭丄乭抩娚偟偨乭忬懺乯偵偍偄偰丄
丂丂旝彫曄壔 丂倓俧丂亖 倁倓俹 亅丂俽倓俿丂偼丄 暵偠偨宯丄壏搙 俿 亖 們倧値倱倲乮堦掕乯丂偲偡傟偽
俽倓俿 偺崁偑徚偊丄 棟憐婥懱偵偮偄偰 倁 亖 俼俿/俹丂傛傝丄椉曈傪愊暘偟偰丄
丂丂嚈俧 亖 亅俼俿 倢値 俹倝丂乮俹倝丗 婥懱 倝 偺暘埑乯 偺宍偲側傝丄丂傑偨丄壔妛億僥儞僔儍儖偺峫偊曽偐傜丄丂嚈俧 亖 亅俼俿 倢値 倎倝 丄丂嚈俧 亖 亅俼俿 倢値 倶倝丂偺傛偆偵丄梟塼乮梈塼乯拞偺妶検傗儌儖暘棪乮擹搙乯偵奼挘偝傟傑偡丅
丂丂偙偺幃傪曄宍偡傞偲丄堦斒揑側壔妛斀墳丂丂兯侾俙侾丂亄丂兯俀俙俀丂亄丂丒丒丒丒丂仺丂兯侾乫俙侾乫丂亄丂兯俀乫俙俀乫丂 亄丂丒丒丒丒丂丂偵偍偗傞 暯峵掕悢 俲倫乮俿乯偑丄師偺 倕亅倶 宆 偺幃偵傛傝昞傢偝傟傑偡丅
丂丂丂丂丂丂丂丂丂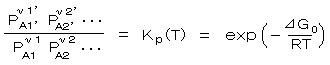
丂丂嚈俧0 偼昗弨惗惉僊僽僘偺帺桼僄僱儖僊乕偲屇偽傟丄俀俆亷偵偍偗傞暔幙侾倣倧倢傪惉暘尦慺偺扨懱偐傜嶌傞嵺梫偡傞僄僱儖僊乕乮俰/倣倧倢乯偱丄斀墳偑偳偪傜曽岦傊偳偺偔傜偄恑
傓偐偺嬱摦椡偺栚埨偵側傝傑偡丅
丂丂嚈俧 亙 侽 側傜偽丄斀墳偼暯峵偵払偡傞傑偱帺敪揑偵婲偙傝傑偡偑丄 傕偟丄嚈俧 亜 侽 側傜偽丄壔妛斀墳偼帺敪揑偵恑峴偣偢丄偙偺斀墳傪恑傔傞偨傔偵偼丄師偺俀偮偺曽朄丄
丂丂丂嘆丂斀墳惗惉暔傪楢懕揑偵丄斀墳偺乭宯奜乭偵攔弌偟 暯峵傪僔僼僩偝偣傞丂丒丒丒丂忲棷丄捑揳丒愅弌丄暘塼丄媧拝丄墦怱暘棧丄側偳丄丂偁傞偄偼丄
丂丂丂嘇丂乭奜晹乭偐傜 揹婥丄岝丄側偳偺僄僱儖僊乕傪梌偊傞丂丒丒丒丂揹婥暘夝丄傔偭偒丒揹婥惛楤丄岝壔妛斀墳丄岝揹抮側偳
偲偄偭偨摿暿側憖嶌偑昁梫偲側傝丄偄偢傟傕乭宯偺奜晹乭偲偺娭傢傝偵傛傝傑偡丅
丂丂偝偰丄偙偺乭宯乭偺斖埻傪峀偘偰丄戝塅拡偺宯傪峫偊偰傒傑偟傚偆丅丂懠偵 暔棟揑側乭奜晹乭傪峫偊傞偙偲偑偱偒側偄偙偺戝塅拡慡懱偼丄帪娫偺宱夁偲嫟偵丄僄儞僩儘僺乕偺憹戝偵傛偭偰旀暰偡傞堦曽偱偡丅乮塅拡婯柾偵側傞偲丄廳椡偺塭嬁偑戝偒偔岠偄偰棃傑偡偑丄僽儔僢僋儂乕儖偼僄儞僩儘僺乕偑嵟戝偵払偟偨寢壥偺堦偮偱偁傝丄塅拡偼偄偮偟偐僽儔僢僋儂乕儖偺乭寠乭偩傜偗偵側偭偰偟傑偄傑偡丅乯
丂丂暓嫵傗僸儞僪僁乕嫵丄僯儏乕僄僀僕側偳偵戙昞偝傟傞 乭揮惗椫夢乭偺峫偊曽偼丄偙偺乽僄儞僩儘僺乕憹戝懃乿偲偄偆尰幚偵偼慡偔儅僢僠偟傑偣傫丅塅拡偵偼丄僄儞僩儘僺乕偑嵟彫偺乭弶傔乭偺忬懺偑偁偭偰丄偦傟偑帪娫偺宱夁偲嫟偵 傛傝棎嶨偵側傞曽岦偵丄晄壜媡揑偵恑峴偟偰偄偔偺偱偡丅乮仺乯
丂丂傑偨丄價僢僌僶儞壖愢傗僀儞僼儔僩儞棟榑傕丄偝傑偞傑側忬嫷徹嫆偵傛傝傑偪偑偄偱偁傝丄僀儞僼儔僩儞棟榑偱偼壖憐揑側乭暔棟揑崅師尦乭偲偄偆傕偺傪愝掕偟側偗傟偽側傜偢丄恖娫偑偑偱偭偪忋偘偨壖憐揑側棻巕丗僀儞僼儔僩儞棻巕
偺専徹傕丄帠幚忋慡偔晄壜擻偱偁傝丄旕忢偵柍棟偺偁傞棟榑乮亖乭暔棟乭棟榑偲偼屇傋側偄棟榑丄婘忋偺嬻榑乯偲側偭偰偄傑偡丅
丂丂偟偨偑偭偰丄惞彂偺婰弎偺捠傝丄栺俇侽侽侽擭慜偺 偁傞抁偄婜娫偱丄恄條偑丄揤抧枩暔傪乽憂憿乿偝傟偨丄偲偄偆僉儕僗僩嫵偺庡挘偺傒偑丄桞堦 惓偟偄塅拡娤偲偟偰巆傝傑偡丅 偙偺戝塅拡丄偡側傢偪丄乭旐憿暔慡懱乭偼丄偝傜偵偦偺乭奜晹乭偱偁傞乭恄條偺椞堟乭偐傜憂傜傟側偗傟偽側傜側偄偺偱偡丅暔棟朄懃傪挻墇偟偨乽婏愓乿丄偡側傢偪丄乽嵞憂憿乿傕丄恄條偵傛傞乭奜晹乭偐傜偺摥偒偐偗偺堦晹偱偡丅丂偦偟偰丄偦偺執戝偝偺掱搙偼丄俢俶俙偑寛偟偰帺慠敪惗揑偵崌惉偝傟側偄偙偲傪峫偊傟偽暘偐傝傑偡丅
丂丂乭偱偼丄偦偺執戝側憂憿庡側傞恄偼丄偄偭偨偄扤偑憿偭偨偺偐両乭偲偄偆栤偄偵偼丄師偺傛偆偵摎偊傞偙偲偑偱偒傑偡丅
丂丂恄條偼丄乽桞堦丄塱墦偺弶傔偐傜丄塱墦偺枹棃傑偱惗偒偰偍傜傟傞曽乿偱偡丅 恄偼乽偙偲偽偺恄乿偱偁傝丄揤抧枩暔偼恄偺偙偲偽偵傛偭偰憿傜傟丄傑偨丄恄偼乽梐尵乿偺帓暔傪梌偊傞曽偱偁傝丄恄條偑岅傜傟偨尵梩偼昁偢帠傪惉偟悑偘傑偡丅丂偡側傢偪丄恄條偺屼慜偱偼偡傋偰偺暔帠偑偡偱偵乽姰椆乿偟偰偄傞偺偱偡丅
丂丂偙偺偙偲傪丄嵟傕抂揑偵昞傢偟偰偄傞帺慠孾帵偼丄弮嫊悢偺巜悢娭悢丂倕 倝兤丂偲偄偆乭柍尷懡壙娭悢乭偱偡丅丂倕 倝兤丂亖 們倧倱 兤 亄 倝 倱倝値 兤丂偼丄怳摦丒攇摦丄揹帴婥丒岝丄検巕椡妛偵尰傟傞悢幃偱偡偑丄嫬奅忦審偺惂尷傪彍偗偽丄亅亣 偐傜 亄亣 傑偱丄偁傞廃婜惈傪傕偭偰柍尷偵孞傝曉偟偰懚嵼偡傞宍幃偱偡丅偦傟偲摨帪偵丄僄僱儖僊乕傪昞傢偟偰偄傑偡丅
丂丂偝傜偵丄偙偺乭弮嫊悢偺巜悢娭悢乭偼丄悢妛偺俁戝暘栰偱偁傞 婔壗妛丄戙悢妛丄夝愅妛偑 偙偺堦偮偺億僀儞僩偵廤寢偟偨宍偱偁傝丄偦傟偧傟偺暘栰傪戙昞偡傞悢妛掕悢 兾丄倝 丄倕 偑偡傋偰娷傑傟偰偄傑偡丅
丂丂擬椡妛丒暔棟壔妛偺 倕亅倶 宆 偺幃丂偼 乽巰乿傪丄偦偟偰丄検巕椡妛偺 倕 倝兤宆偺幃 偼 乽塱墦偺偄偺偪乿傪丄偦傟偧傟昞尰偟偰偄傑偡丅
丂丂偙偺傛偆偵丄帺慠孾帵偵傛偭偰丄旐憿暔偼乽憂憿庡乿偺屼惈幙傪斀塮偟丄 帺慠懳悢偺掙 倕 偑丄偦偺惗巰傪暘偗傞崻尮偵側偭偰偄傞偙偲偑暘偐傝傑偡丅 宍帶忋妛揑偵尵偊偽丄偙偺 倕 偙偦丄乽屼巕僀僄僗丒僉儕僗僩乿偱偡丅僀僄僗丒僉儕僗僩偼丄乽嵞椪乿偺帪丄惗偒偰偄傞幰偲巰傫偱偄傞幰偲傪嵸偐傟傑偡丅
兾偼乽屼晝乿丄 倝 偼乽惞楈條乿 傪昞傢偟丄恄偺乽嶰埵堦懱乿偑偙偙偵孾帵偝傟傑偡丅
丂丂丂乮嶲峫儁乕僕乯丂丂丂係丏 暔棟壔妛偺 倕丂丟丂丂俀丏暓嫵丒僸儞僪僁乕嫵偲帺慠孾帵丄丂俇丏悢妛巚嶕偺晄巚媍丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂栠傞丂丂丂丂丂丂丂丂丂丂丂丂僩僢僾傊栠傞